2452. Sticks Problem
Xuanxuan has n
sticks of different length. One day, she puts all her sticks in a line,
represented by s1, s2, s3, ...sn. After measuring the length of each stick sk
(1 ≤ k ≤ n), she finds that for some sticks si and sj (1 ≤ i
< j ≤ n), each stick placed between si and sj is longer than si but
shorter than sj.
Now given the length of s1, s2, s3, ...sn, you are required to find the maximum value j – i.
Input. The input contains multiple test cases. Each case
contains two lines.
Line 1: a single integer n (n
≤ 50000), indicating the number of sticks.
Line 2: n different positive integers (not
larger than 100000), indicating the length of each stick in order.
Output. Output the maximum value j – i in a single line. If there
is no such i and j, just output -1.
Sample Input
4
5 4 3 6
4
6 5 4 3
Sample
Output
1
-1
РЕШЕНИЕ
структуры данных – RMQ + бинарный поиск
Анализ алгоритма
Для каждого индекса i находим максимальный индекс k (i ≤ k ≤ n), для которого RMinQ(si+1, …, sk) > si, бинарным поиском. Искомым j будет индекс, на котором достигается RMaxQ(si,
…, sk) (i ≤ j ≤ k).
Таким образом следует для
каждого индекса i найти максимальный
возможный индекс j и среди всех таких пар (i, j) вычислить максимальную
разность j – i.
Пример
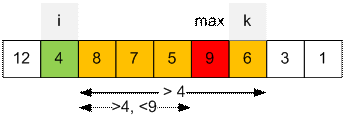
Пусть i = 2 (s2
= 4). Наибольшим является индекс k = 7, для которого RMinQ(si+1, …, sk)
> 4. RMaxQ(s3, …, s7) достигается на индексе j
= 6.
Реализация алгоритма
#include <cstdio>
#include <algorithm>
#define MAX 50010
#define LOGMAX 16
using namespace
std;
int dp_max[MAX][LOGMAX],
dp_min[MAX][LOGMAX];
int a[MAX];
int i, j, n, res;
void Build_RMQ_Array(int *b)
{
int i, j;
for (i = 1; i <= n; i++)
{
dp_min[i][0] =
b[i];
dp_max[i][0] = i;
}
for (j = 1; 1 << j <= n; j++)
for (i = 1; i + (1 << j) - 1 <= n; i++)
{
if (b[dp_max[i][j - 1]] > b[dp_max[i + (1 <<
(j - 1))][j - 1]])
dp_max[i][j] =
dp_max[i][j - 1];
else
dp_max[i][j] =
dp_max[i + (1 << (j - 1))][j - 1];
dp_min[i][j] =
min(dp_min[i][j
- 1], dp_min[i + (1 << (j - 1))][j - 1]);
}
}
int RangeMaxQuery(int i, int j)
{
int k = 0;
while ((1 << (k + 1)) <= j - i + 1) k++;
if (a[dp_max[i][k]] > a[dp_max[j - (1<<k) +
1][k]])
return dp_max[i][k];
else
return
dp_max[j - (1<<k) + 1][k];
}
int RangeMinQuery(int i, int j)
{
int k = 0;
while ((1 << (k + 1)) <= j - i + 1) k++;
return min(dp_min[i][k],dp_min[j - (1<<k) +
1][k]);
}
int BinSearch(int
Left, int Right)
{
int MinValue = a[Left++];
if (RangeMinQuery(Left,Right) > MinValue) return Right;
while (Right > Left)
{
int Middle = (Left + Right) / 2;
if (RangeMinQuery(Left,Middle) > MinValue)
Left = Middle +
1;
else
Right = Middle;
}
if (dp_min[Left][0] <= MinValue) Left--;
return Left;
}
int main(void)
{
while(scanf("%d",&n)
== 1)
{
for(i = 1; i <= n; i++) scanf("%d",&a[i]);
Build_RMQ_Array(a);
res = 0;
for(i = 1; i <= n; i++)
{
j = BinSearch(i,
n);
j =
RangeMaxQuery(i,j);
if (j - i > res) res = j - i;
}
if (res == 0) res = -1;
printf("%d\n",res);
}
return 0;
}